如图,直线y=-x+b(b>0)与双曲线(x>0)交于A,B两点,连接OA,OB,AM⊥y轴于M,BN⊥x轴于N.有以下结论:
①OA=OB;②△AOM≌△BON;;③若∠AOB=45°,则S_△AOB=k④当AB=时,ON-BN=1.其中结论正确的个数为( )

解：设A（x₁，y₁），B（x₂，y₂），代入y=中，得x₁•y₁=x₂•y₂=k，
联立，得x²-bx+k=0，
则x₁•x₂=k，又x₁•y₁=k，
∴x₂=y₁，
同理可得x₁=y₂，
∴ON=OM，AM=BN，
∴△AOM≌△BON，OA=OB，①②正确；
③如图，作OH⊥AB于H，

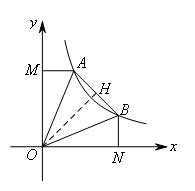
易证∠MOA=∠BON=∠AOH=∠BOH=22.5°，
△OAM≌△OAH≌△OBH≌△OBN，
∴S_△AOB=S_△AOM+S_△BON=k+k=k，③正确；
④如图，延长MA，NB交于G点，

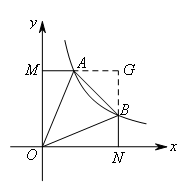
易证GB=GA，△ABG为等腰直角三角形，
当AB=时，GA=GB=1，
∴ON-BN=GN-BN=GB=1，④正确．
正确的结论有4个．
故选D

略