如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论:①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH,④AD2=OD•DH中,正确的是( )
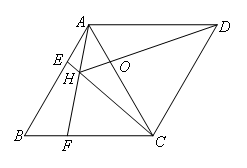
- A.①②④
- B.①②③
- C.②③④
- D.①②③④
答案
正确答案:D
知识点:相似三角形的判定与性质 菱形的性质 全等三角形的判定与性质
易证△ABF≌△CAE,故①正确;∴∠BAF=∠ACE,∵∠AEH=∠B+∠BCE,∴∠AHC=∠BAF+∠AEH=∠BAF+∠B+∠BCE=∠B+∠ACE+∠BCE=∠B+∠ACB=60°+60°=120°;故②正确;延长CE至点M,使得HM=HA,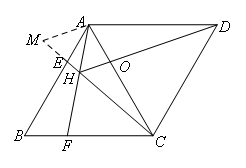 易得△AHM为等边三角形,△DAH≌△CAM,∴DH=CM=HM+HC=AH+CH,故③正确;由△DAH≌△CAM得∠AHD=∠M=∠DAO=60°,又∵∠ODA=∠ADH,∴△OAD∽△AHD,∴
易得△AHM为等边三角形,△DAH≌△CAM,∴DH=CM=HM+HC=AH+CH,故③正确;由△DAH≌△CAM得∠AHD=∠M=∠DAO=60°,又∵∠ODA=∠ADH,∴△OAD∽△AHD,∴![]() ,∴AD2=OD•DH.故④正确.故选D.
,∴AD2=OD•DH.故④正确.故选D.
略








