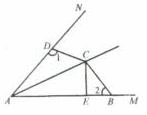
如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且AE=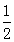 (AD+AB).则∠1和∠2的关系是( )
(AD+AB).则∠1和∠2的关系是( )
- A.∠1=2∠2
- B.∠1=3∠2
- C.∠1=90°+∠2
- D.∠1+∠2=180°
答案
正确答案:D
知识点:三角形的角平分线、中线和高 角平分线的性质
AE=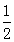 (AD+AB),由图可知,AD<AE<AB.在AE上截取AF=AD,连接CF.在△ACD和
(AD+AB),由图可知,AD<AE<AB.在AE上截取AF=AD,连接CF.在△ACD和
△ACF中,AD=AF,∠DAC=∠FAC,AC边公用, ∴△ACD≌△ACF(SAS),∴∠1=∠AFC.
∵AE=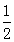 (AD+AB),AD=AF,AE=AF+FE,AB=AF+FB, ∴AF+FE=
(AD+AB),AD=AF,AE=AF+FE,AB=AF+FB, ∴AF+FE=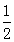 (AF+
(AF+
AF+FB),整理得FB=2EF,即CE为△BCF中边FB的中线. 又∵CE⊥FB,即中线与高重合,
∴△BCF为等腰三角形,∴∠2=∠BFC. ∠AFC+∠BFC=180°,∴∠1+∠2=180°.

角平分线与全等不会灵活运用。







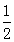 (AD+AB).则∠1和∠2的关系是( )
(AD+AB).则∠1和∠2的关系是( )
