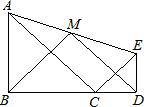
如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=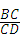；②S_△ABC+S_△CDE≥S_△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（　　　　）

∵△ABC和△CDE均为等腰直角三角形，∴AB=BC，CD=DE，∴∠BAC=∠BCA=∠DCE=∠DEC=45°，∴∠ACE=90°；∵△ABC∽△CDE∴==①∴tan∠AEC=，∴tan∠AEC=；故本选项正确；②∵S_△ABC=a²，S_△CDE=b²，S_梯形ABDE=（a+b）²，∴S_△ACE=S_梯形ABDE﹣S_△ABC﹣S_△CDE=ab，S_△ABC+S_△CDE=（a²+b²）≥ab（a=b时取等号），∴S_△ABC+S_△CDE≥S_△ACE；故本选项正确；④过点M作MN垂直于BD，垂足为N．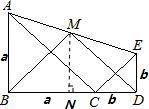
∵点M是AE的中点，则MN为梯形中位线，∴N为中点，∴△BMD为等腰三角形，∴BM=DM；故本选项正确；③又MN=（AB+ED）=（BC+CD），∴∠BMD=90°，即BM⊥DM；故本选项正确．

对三角函数的定义掌握不熟练