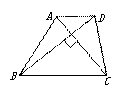
如图，在梯形ABCD中，AD∥BC，对角线AC⊥BD，若AD=3，BC=7，则梯形ABCD面积的最大值为（）

解：过点D作DE∥AC交BC的延长线于点E则四边形ACED为平行四边形，从而CE=AD=3∴∴梯形ABCD的面积=△BDE的面积∵AC∥DE，AC⊥BD∴BD⊥DE∴又BE=BC+CE=7+3=10得：当BD=DE时面积最大，从而最大面积为25

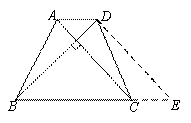
高的范围定义错，做完辅助线的时候没有进行面积的转化