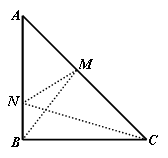
在△ABC中,∠ABC=90°,AB=BC=4,在AC上找点M,在AB上找点N,使得BM+MN+NC最短,则最短值为().
- A.4
- B.

- C.
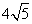
- D.8
答案
正确答案:C
知识点:轴对称的性质
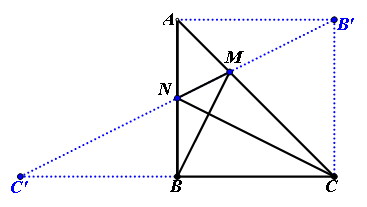
解:分别作点B关于AC的对称点B',点C关于AB的对称点C',连结C'、B'交AC、AB于M、N两点,此时BM+MN+NC最小且最小值为B' C'的长度。连结AB'、CB',∵△ABC为等腰直角三角形,B'为B关于AC的对称点∴AB'=AB=BC=CB'∵∠ABC=90°∴四边形ABCB'为正方形∴CB'=4,∠BCB'=90°∵C'为C关于AB的对称点∴BC' =BC=4在Rt△B'CC'中,![]() ∴BM+MN+NC的最小值为
∴BM+MN+NC的最小值为![]()
对称性质的应用,辅助线的做法。







