如图，矩形ABCD中，AB=4cm，BC=8cm，动点M从点D出发，按折线DCBAD方向以2cm/s的速度运动，同时动点N从点D出发，按折线DABCD方向以１cm/s的速度运动，相遇时停止运动．设运动的时间为t秒．
（1）t为何值时，两点相遇？
（2）若点E在线段BC上，BE=1cm，当点M在BC边上时，
①t为何值时，以A、E、M、N为顶点的四边形是平行四边形？
②t为何值时，以A、E、M、N为顶点的四边形是等腰梯形？
答案
解：（1）∵矩形ABCD的周长为24cm
∴t+2t=24，t=8
∴t=8时两点相遇．
（2）
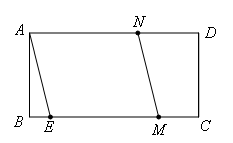
①∵点M在线段BC上
∴
如图，当
时
∵AN与EM平行
∴只需AN=EM即可．
∵ND=t，DC+CM=2t
∴AN=8-t，CM=2t-4
∵BE=1
∴EC=7，EM=EC-MC=11-2t
∴8-t=11-2t
∴t=3
当
时，
∵AN与EM平行
∴只需AN=EM即可
∵ND=t，DC+CM=2t
∴AN=8-t，CM=2t-4
∵BE=1
∴EC=7，EM=MC-EC=2t-11，
∴8-t=2t-11∴t=
（舍去）
∴当t=3时，点A、E、M、N组成平行四边形．
②∵点M在边BC上
∴
当时，AN与EM平行，只需AE=NM即可．
过点N作NF⊥BC于点F，则BE=MF，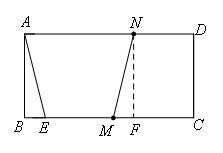
∵ND=t，CM=2t-4，CF=ND=t
∴MF=t-4
∵BE=1
∴1=t-4
∴t=5
当时，AN与EM平行，只需AM=EN即可．
过点N作NF⊥BC于点F，则BM=EF，
∵ND=t，CM=2t-4，CF=ND=t
∵BE=1
∴EC=7，EF=7-t，BM=BC-CM=12-2t，
∴7-t=12-2t
∴t=5（舍去）
综上所述，当t=5时，点A、E、M、N组成等腰梯形．
知识点：四边形中的动点、存在性问题
略
略
WORD格式（
