如图,梯形ABCD中,AD∥BC,∠C=30°,AD=8cm,CD=16cm,BC=28cm.点P、Q分别是梯形某边上同时出发的动点,当其中一个动点到达端点停止运动时,另一个动点随之停止运动,其中点P移动的速度是1cm/s,点Q移动的速度是2cm/s.
(1)在图1中,点P从点A出发向点D移动,点Q从点C出发向点B移动,设移动的时间为t秒,t为何值时,四边形PQCD为平行四边形?
(2)在图2中,点P从点A出发向点D移动,点Q从点C出发向点D移动,设移动的时间为t秒,用关于t的式子表示△PQB的面积,并求出t的取值范围.


答案
解:(1)由题意得:![]()
∵PD∥CQ
∴当PD=CQ,四边形PQCD为平行四边形
∵AP=t,CQ=2t
∴PD=8-t
∴8-t=2t,t=![]()
∴当t=![]() 时,四边形PQCD为平行四边形
时,四边形PQCD为平行四边形
(2)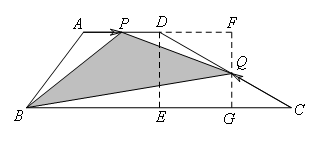
如图,过点D作DE⊥BC于点E,过点Q分别作QF⊥AD延长线于点F,QG⊥BC于点G.
由题意得:![]()
![]()
∵∠C=30°,CQ=2t,AD=8,AP=t,CD=16,BC=28
∴QG=t,PD=8-t,DQ=16-2t,∠QDF=30°
∴QF=8-t,DE=8
∴![]() =
=![]() (AD+BC)
(AD+BC)![]() DE=144
DE=144
![]() =
=![]() AP
AP![]() DE=4t
DE=4t
![]() =
=![]() PD
PD![]() QF=
QF=![]()
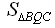 =
=![]() BC
BC![]() QG=14t
QG=14t
∴![]() =
=![]() (
(![]() )
)
知识点:四边形中的动点、存在性问题
略
略









