如图，分别以△ABC的边AC，BC为一边向外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半．
答案
证明：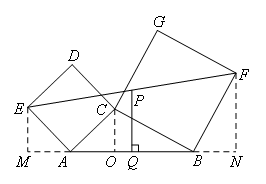
分别过点E，C，F作AB的垂线，分别交AB或AB的延长线于点M，O，N，则可得到四边形EMNF是直角梯形，PQ是它的中位线∴PQ＝
(EM＋FN)
∵∠EAC＝90°
∴∠EAM＋∠CAO＝90°
∵∠EAM＋∠AEM＝90°
∴∠CAO＝∠AEM
∵CA＝AE，∠M＝∠AOC
∴△CAO≌△AEM
∴AO＝EM
同理可得：△BOC≌△FNB，BO＝FN
∴PQ＝(EM＋FN)＝(AO＋BO)＝AB
即：点P到AB的距离是AB的一半．
知识点：中点问题
略
略
WORD格式（
