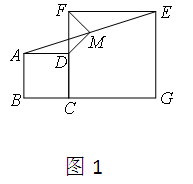
如图1,在正方形ABCD和正方形CGEF(CG>BC)中,点B、C、G在同一直线上,点M是AE的中点.(2)将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF的对角线CE恰好与正方形ABCD的边BC在同一条直线上,如图2,原问题中的其他条件不变,则(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
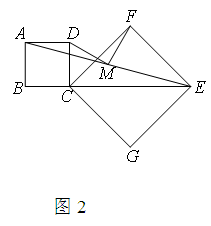
小明观察到第2问其实是在第1问的基础上旋转了其中一个正方形得到了,认识到这是个类比探究的题目,所以类比第一问的做法来思考问题:首先观察到在图形旋转过程中,点M始终是AE的中点,依然考虑( ),连接DF,FN后,如图,要证明DM⊥MF且DM=MF,只需证明DF=FN且DF⊥FN即可,小明先证明出△ADM≌△ENM,然后充分利用题干中的条件,用( )证明出△CDF≌△ENF,从而得到DF=FN,DF⊥FN,证明出结论
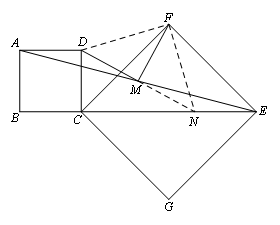
①倍长中线;②类倍长中线;③三线合一;④SAS;⑤AAS;⑥ASA;⑦HL以上括号填写的顺序为( )
- A.①⑤
- B.②⑥
- C.②④
- D.③④
答案
正确答案:C
知识点:类比探究问题
略
略










