（2011安徽）如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD= $2\sqrt{2}$ ，CD= $\sqrt{2}$ ，点P在四边形ABCD的边上，若P到BD的距离为 $\frac{3}{2}$ ，则点P的个数为( )

答案

正确答案：B

解：当点P在BD的左端，即AB和AD上运动时，P到BD的最小距离为0，P到BD的最大距离为当点P运动到A点的时候，此时由AB=AD= $2\sqrt{2}$ ，得：△ABD为等腰直角三角形，从而A到BD的距离为等腰三角形斜边上的高，为2
∵ $\frac{3}{2}<2$
∴存在两个点
当点P在BD的右端，即AB在DC和BC上运动时，P到BD的最小距离为0，P到BD的最大距离为当点P运动到点C的位置，即点C到BD的距离，如图，即CE的长

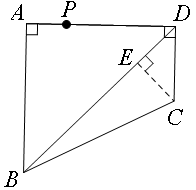
∵∠ADB=45°，∠ADC=90°
∴∠CDB=45°
∴△CDE为等腰直角三角形
从而CE= $\frac{CD}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2}}=1$
∵ $1<\frac{3}{2}$
∴此时不存在符合要求的点Ｐ
综上：点Ｐ的个数为２，Ｂ选项正确

分类讨论时忘记一种情况

下载次数：1

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>

（2011安徽）如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=，CD=，点P在四边形ABCD的边上，若P到BD的距离为，则点P的个数为( )

答案

（2011安徽）如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD= $2\sqrt{2}$ ，CD= $\sqrt{2}$ ，点P在四边形ABCD的边上，若P到BD的距离为 $\frac{3}{2}$ ，则点P的个数为( )