如图所示，四边形ABCD是正方形，点E是边BC的中点且∠AEF=90°，EF交正方形外角平分线CF于点F，取边AB的中点G，连接EG.（1）求证：EG=CF；（2）将△ECF绕点E逆时针旋转90°，请在图中直接画出旋转后的图形，并指出旋转后CF与EG的位置关系.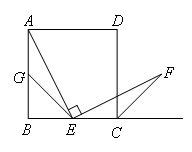

答案

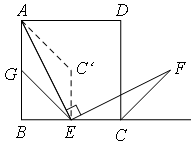（1）证明：∵正方形ABCD点G，E为边AB、BC中点∴AG=EC又∵CF为正方形外角平分线且∠AEF=90°，BG=BE∴∠AGE=∠E∠GAE=∠FEC∴△AGE≌△ECF∴EG=CF（2）如图，旋转后CF与EG的位置关系为平行即CF∥EG

知识点：正方形的性质  旋转的性质  

略

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>