（2010盐城）小明尝试着将矩形纸片ABCD（如图①，AD>CD）沿过A点的直线折叠，使得B点落在AD边上的点F处，折痕为AE（如图②）；再沿过D点的直线折叠，使得C点落在DA边上的点N处，E点落在AE边上的点M处，折痕为DG（如图③）．如果第二次折叠后，M点正好在∠NDG的平分线上，那么矩形ABCD长与宽的比值为（）

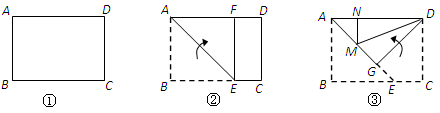
A. $\frac{2\sqrt{3}}{3}$
B.2
C. $\sqrt{3}$
D. $\sqrt{2}$

答案

正确答案：D

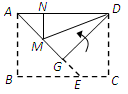
解：折叠前后的两个图形是全等的
设EC=x，则MN=x
∵第二次折叠后，M点正好在∠NDG的平分线上
∴MN=MG（角平分线上的点到角两边的距离相等）
从而MG=GE=x
∵△ANM为等腰直角三角形
∴AM= $\sqrt{2}$ MN= $\sqrt{2}$ x
∴AE=AM+MG+GE= $\sqrt{2}$ x+x+x=（ $\sqrt{2}$ +2）x
∴AB=BE= $\frac{(\sqrt{2}+2)x}{\sqrt{2}}=(1+\sqrt{2})x$
BC=BE+EC= $(\sqrt{2}+2)x$
∴矩形ABCD的长与宽比值= $\frac{BC}{AB}=\sqrt{2}$

折叠前后的对应关系

下载次数：3

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>