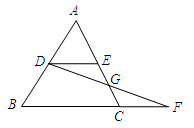
如图：在△ABC中，D，E分别是AB和AC的中点，F是BC延长线上一点，DF平分CE于点G，CF=1，则BC的长，△ADE与△ABC的周长之比，△CFG与△BFD的面积之比分别是（ ）
- A.2；1:2；1:6
- B.2；1：2；1：4
- C.3；1：3；1：6
- D.3；1:2；1:4
答案
正确答案：A
∵D、E分别是AB和AC的中点
∴DE∥BC，DE= 12BC
∴△ADE∽△ABC，△GED≌△GCF
∴DE=CF=1
∴CF= 12BC
∴BC=2
∴△ADE与△ABC的周长之比为DE：BC=1：2；
∵△ADE与△ABC的面积之比为1：4；
∴△ADE与四边形DECB的面积之比为1：3；
∵△ADE与△DEG的面积之比为2：1；
∴△CFG与△BFD的面积之比为1：6．
没有找到相似的三角形，对三角形的中位线应用不熟悉
WORD格式（
