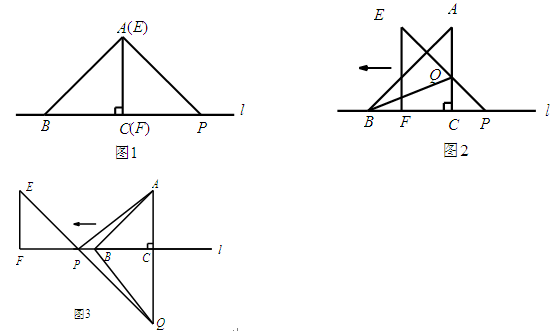如图,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)请你通过观察,测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ,猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
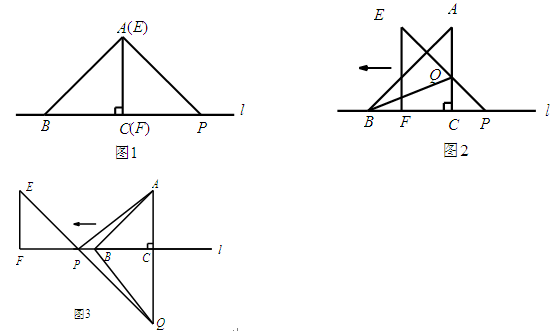
答案
解:(1)AB与AP垂直且相等
证明:∵AC=BC,AC=CP,∴BC=PC
在△ACB和△ACP中
∴△ACB≌△ACP(SAS)
∴AB=AP,∠ABC=∠APC=45°
∴∠BAP=90°,即AB⊥AP。
(2)BQ与AP垂直且相等
证明:延长BQ交AP于点G。
因为∠QPC=45°,而∠QCP=90°,∴∠PQC=45°,
∴CP=CQ
在△BCQ和△ACP中
∴△BCQ≌△ACP(SAS)
∴BQ=AP,∠PAC=∠QBC
∵∠AQG=∠BQC,∠BQC+∠QBC=90°
∴∠PAC+∠AQG=90°,即BQ⊥AP
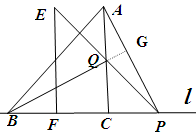
(3)成立。
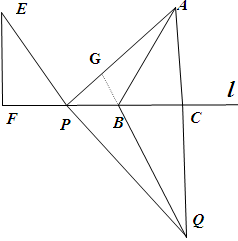
证明:延长QB交AP于点G。
∵∠EPF=∠QPC=45°,∠QCP=90°,
∴∠PQC=45°,∴CP=CQ
在△APC和△QBC中
∴△APC≌△QBC(SAS)
∴BQ=AP,∠AQB=∠APC
∵∠AQP+∠CPQ=90°,∴∠APC+∠AQG+∠GQP=90°
∴∠APB+∠BPQ+∠GQP=90°
∴∠QGP=90°即QB⊥ AP。
知识点:全等三角形的判定与性质
图形运动时要分析清楚等量关系。
分析清楚运动过程,寻找等量关系