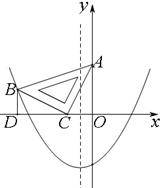
（2011年青海西宁）在平面直角坐标中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点C为（-1,0）.如图所示，B点在抛物线图像上，过点B作BD⊥x轴，垂足为D，且B点横坐标-3.（1）求证：△BDC≌△COA；（2）求BC所在直线的函数关系式；（3）抛物线的对称轴上是否存在点P，使△ACP是以AC为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．

答案

解：（1）∵∠BCD+∠ACO=90°，∠ACO+∠CAO=90°，
∴∠BCD=∠CAO．
∵△ABC是等腰直角三角形，
∴BC=AC．
又∵∠BDC=∠COA，
∴△BCD≌△CAO(AAS)
（2）∵C点坐标为（-1,0），
∴BD=CO=1．
∴B点坐标为（-3,1）．
设直线BC的解析式为：y=kx+b，
则：，解得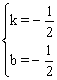
∴直线BC的解析式是：y=x．
(3)存在．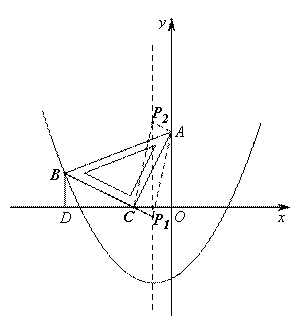

抛物线解析式为：y==．
∴抛物线的对称轴为：．
若以AC为直角边，点C为直角顶点，对称轴上有一点P₁，使CP₁  ⊥AC，
∵BC⊥AC，
∴点P₁是直线BC与对称轴直线的交点．
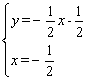，解得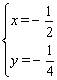
∴点P₁为（，）．
若以AC为直角边，点A为直角顶点，对称轴上有一点P₂，使AP₂⊥AC，则过点A作AP₂∥BC，交对称轴直线于点P₂．
∵CD=AO，
∴点A(0,2)，
又∵直线BC的斜率为：k=,
∴直线AP₂的解析式为：y=x+2．
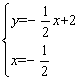，解得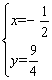
∴点P₂为（，）
∴点P的坐标分别为：（，）、（，）．

知识点：二次函数动点问题  

略

略

下载次数：6

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>