（2011辽宁大连）如图，抛物线y＝ax²+bx+c经过A（－1，0）、B（3，0）、C（0，3）三点，对称轴与抛物线相交于点P、与直线BC相交于点M，连接PB．（1）求该抛物线的解析式；（2）抛物线上是否存在一点Q，使△QMB与△PMB的面积相等，若存在，求点Q的坐标；若不存在，说明理由；（3）在第一象限、对称轴右侧的抛物线上是否存在一点R，使△RPM与△RMB的面积相等，若存在，直接写出点R的坐标；若不存在，说明理由．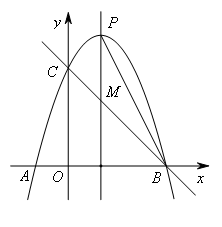

答案

解：（1）设抛物线的解析式为：y=ax²+bx+c（a≠0），
∵抛物线经过点A（－1，0）、B（3，0）、C（0，3）,
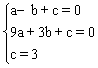∴，解得
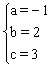
∴二次函数式为y=-x²+2x+3；
（2）由y=-x²+2x+3=-（x-1）²+4，
则顶点P（1，4），对称轴是：x=1．
由B，C两点坐标可知，直线BC解析式为y=-x+3，点M点坐标为（1,2）

设过点P与直线BC平行的直线为：y=-x+b，
将点P（1，4）代入，得y=-x+5，
将y=-x+5代入抛物线y=-x²+2x+3中，
-x²+2x+3=-x+5，解得x=1或x=2，
代入y=-x+5，则得点Q（1，4）或（2，3），
点Q（1，4）与P重合，
∴点Q（2，3），
设PM与x轴交点为P′，而M（1，2），
∴PM=MP′=2，
设过P′（1，0）且与BC平行的直线为y=-x+c，
将P′代入，得y=-x+1，
，解得x=或x=
∴Q（2，3）或（，）或（，）；
（3）要使△RPM与△RMB的面积相等，则点P到MR的距离等于点B到MR的距离．
由点M（1,2），P（1,4），
PM=P’M可知：点R存在，即过点M平行于x轴的直线:y=2，
代入抛物线y=-x²+2x+3中得：x=或x=（在对称轴的左侧，舍去），
∴点R（，2）．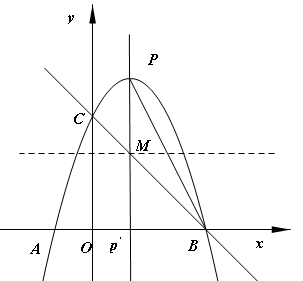

知识点：中考压轴之函数类问题  

略

略

下载次数：19

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>