如图，四边形ABCD为矩形，C点在x轴上，A点在y轴上，D点坐标是（0，0），B点坐标是（3，4），矩形ABCD沿直线EF折叠，点A落在BC边上的G处，E、F分别在AD、AB上，且F点的坐标是（2，4）．（1）求G点坐标；（2）求直线EF解析式.

答案

解：（1）由轴对称性质，得FG=AF=2,BF=AB-AF=1，
在Rt△BFG中，
∵B点坐标是（3，4），
∴BC=4
∴
∴G点坐标为（3，）
（2）如图，过点E作EH⊥BC，垂足为H，则EH=3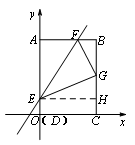

设AE=t，则EG=t，GH=BH-BG=t-.
在Rt△HEG中，EH²+GH²=EG²，
即
∴
∴点E的坐标为（0，）
设直线EF解析式为y=kx+b，
将点E（0，），F（2，4）代入，
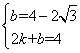得解之，得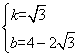
∴直线EF解析式为.

知识点：求解一次函数表达式  

略

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>