如图，在直角坐标系中，抛物线y=a+bx+c(a0)与x轴交于A(-1,0),B(3,0)两点，抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M,N两点，过线段MN上一点P作y轴的平行线交抛物线于点Q.
（1）求抛物线的解析式及顶点D的坐标；（2）问点P在何处时，线段PQ最长，最长为多少？（3）设E为线段OC上的三等分点，连接EP,EQ，若EP=EQ时，求点P的坐标.

答案

解：（1）∵抛物线与x轴交于A（-1,0）、B（3,0）两点,交y轴于点C（0,3）,
由题意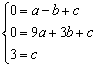得解得
抛物线的解析式为：
∴，
∴ 点D的坐标（1,4）；
（2）∵PQ⊥x轴，∴P,Q的横坐标相同，
∵P点在直线y=x-1上，设P（a,a-1）,则Q（a,）
∴PQ=，
当时，线段PQ的值最大为，则P点坐标为（，）
（3）∵E为线段OC上的三等分点，且OC＝3,
∴E(0,1)或E（0,2）,
设P(p,p-1)(在y=x-1上)，则Q（p,）.
当E（0,1）时，∵EP=EQ
∴,
∴,
∴,
①当时，
∴,
∴p=0或3,
当p=0,P(0,-1),Q(0,3),
当P=3,P(3,2),Q(3,0),
∵直线y=x-1交抛物线于点M、N两点，
∴,
解得：，M的横坐标为，N点的横坐标为，
∴P点的横坐标：，
∴P（3,2）,Q(3,0)不符合要求舍去；
②p²-2p-2=-p+2时
∴p²-p-4=0，，
∴此种情况不符合要求舍去；当E（0,2）时，
∵EP=EQ,
∴，

③当时，
∴
∴p=1或2
当p=1时,P(1,0),Q(1,4)
当p=2时,P(2,1),Q(2,3)
④,
解得：（不符合题意，舍去）
综上所述，P点的坐标为：（1,0）,（2,1）,（0,-1）

知识点：二次函数综合题  

略

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>