（2011广东清远）如图，抛物线y＝(x＋1)2＋k与x轴交于A、B两点，与y轴交于点C(0，－3)．
（1）求抛物线的对称轴及k的值；
（2）抛物线的对称轴上存在一点P，使得PA＋PC的值最小，求此时点P的坐标；
（3）点M是抛物线上一动点，且在第三象限.
①当M点运动到何处时，△AMB的面积最大？求出△AMB的最大面积及此时点M的坐标；
②当M点运动到何处时，四边形AMCB的面积最大？求出四边形AMCB的最大面积及此时点M的坐标．
答案
（1）抛物线的对称轴为直线x=-1,把C(0,-3)代入y＝(x＋1)2＋k得-3＝1+k∴k=-4
(2)连接AC，交对称轴于点P,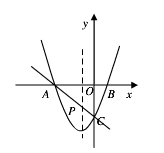
∵y＝(x＋1)2-4,
令y=0,
可得(x＋1)2-4＝0
解得：
，
∴A(-3,0),B(1,0)
设直线AC的关系式为y=mx+b
把A（-3,0）,C（0,-3）代入y=mx+b得，
-3m+b=0 b=-3
∴m=-1
∴直线AC的关系式为y=-x-3
当x=-1时，y=1-3=-2
∴P(-1,-2)
(3)①设M的坐标为（x, (x＋1)2-4）
∴
当x=-1时，S最大，最大值为S＝8
M的坐标为（-1,-4）
②过M作x轴的垂线交于点E,连接OM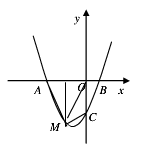
当
时，S最大，最大值为
此时，M的坐标为
知识点：二次函数的应用
略
略
WORD格式（
