如图，正方形ABCD中，AB=6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③AG∥CF；④S_△FGC=3.其中正确结论是           ，并给出证明.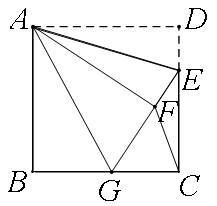

答案

正确结论是①②③，证明如下：
在正方形ABCD中，AB=AD=BC=CD，∠B=∠BCD=∠D=90°
由轴对称的性质可得：DE=EF，AF=AD，∠AFE=∠D=90°
在Rt△ABG与Rt△AFG中，
AF=AB，∠AFG=∠B=90°，AG=AG
∴△ABG≌△AFG——————①正确
∴BG=FG，∠AGB=∠AGF
∵AB=6，CD＝3DE
∴DE=2
设BG=x，则CG=BC-BG= 6-x
GE=GF+EF=BG+DE=x+2
在Rt△ECG中，CG²+CE²=EG²
而CG=6-x，CE=4，EG=x+2
∴(6-x) ²+ 4² = (x+2) ²
解得：x=3
∴BG=GF=CG=3————②成立
∵CG=GF
∴∠CFG=∠FCG
∵∠BGF=∠CFG+∠FCG（三角形的外角等于不相邻的两个内角和）
而∠BGF=∠AGB+∠AGF
可得：∠CFG+∠FCG=∠AGB+∠AGF
∵∠AGB=∠AGF，∠CFG=∠FCG
∴2∠AGB=2∠FCG
即∠AGB=∠FCG
∴AG//CF————③正确
在△CFG和△CEG中，分别把FG和GE看作底边，则这两个三角形的高相同。
那么，S△CFG：S△CEG=FG：GE= 3：5
S△CEG=CG×CE÷2=3×4÷2=6
所以，S△CFG=S△CEG==--------④不正确

知识点：四边形折叠  

略

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>