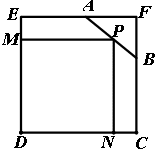
如图，已知边长为4的正方形钢板，有一个角锈蚀，其中AF=2，BF=1，为了合理利用这块钢板，将在五边形EABCD内截取一个矩形MDNP，使点P在AB上．问：这样截取的矩形面积能否达到12?若能请求出P的位置，若不能请说明理由．
答案
如图所示，为了表达矩形MDNP的面积，过点P作PQ⊥EF，设 PM＝x，则2≤x≤4，
∵∠QAP=∠FAB，∠AQP=∠AFB=90°，∴△AQP∽△AFB，∴，AQ=EQ-EA=MP-EA=x-2，∴QP=
，∴PN=QN-QP=4-
=
，
∴矩形MDNP的面积S=PM·PN=，根据题意S=12，
∴，解得x=4或x=6，又∵2≤x≤4，所以x=4，即MP=4，存在P点，点P与B点重合。
根据题意设PM=x，用x表示出PN，列出面积函数。再求解。
不会根据方程列方程解决问题。
WORD格式（
