如图，以平行四边形ABCD的BC，CD为边在四边形内侧作等边△BCE和等边△CDF，连接AE，EF，AF.求证：△AEF为等边三角形.
答案
证明：如图，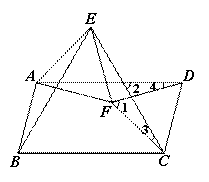
∵四边形ABCD为平行四边形
∴AD=BC，AD∥BC
∵△BCE和△CDF均为等边三角形
∴BC=CE，CF=DF，∠BCE=∠1=60°
∴AD=CE
∵AD∥BC
∴∠2=∠BCE=60°
∴∠1=∠2=60°
∴∠3=∠4
∴△FCE≌△FDA
∴EF=AF
∴△AEF为等腰三角形
∴∠CFE=∠DFA
∴∠CFE-∠DFE=∠DFA-∠DFE 即：∠AFE=∠1=60°
∴△AEF为等边三角形
知识点：作等边三角形
略
略
WORD格式（
