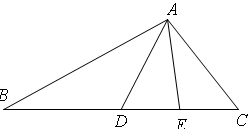
如图，△ABC中，BD=DC=AC,E是DC的中点，求证，AD平分∠BAE.

答案

 
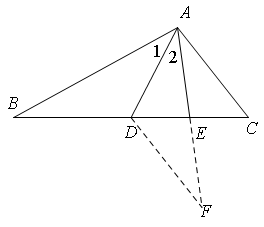
证明：延长AE到F，使EF=AE，连接DF
在△ACE和△FDE中，

∴△ACE≌△FDE（SAS）、
∴AC=DF，∠C=∠CDF
∵AC=CD
∴∠DAC=∠ADC
从而∠DAC+∠C=∠ADC+∠CDF=∠ADF
∵∠ADB为△ACD的一个外角
∴∠ADB=∠C+∠DAC
即∠ADB=∠ADF
在△ABD和△AFD中

∴△ABD≌△AFD（SAS）
∴∠1=∠2
即AD平分∠BAE

知识点：全等三角形的判定  

看到中点，想到倍长中线，构造出全等三角形，实现线段和角度的转移，从而得到解决

倍长中线

下载次数：6

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>