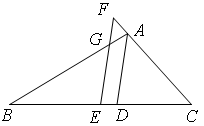
如图，在△ABC中，AD交BC于点D，点E是BC中点，EF∥AD交CA的延长线于点F，交EF于点G，若BG=CF，求证：AD为△ABC的角平分线.

答案

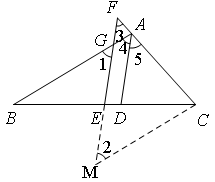
证明：延长GE到M，使EM=GE，连接CM
在△BEG和△CEM中，

∴△BEG≌△CEM（SAS）
∴∠1=∠2，BG=CM
又∵BG=CF
∴CM=CF，即∠2=∠3
∵EF∥AD
∴∠1=∠4，∠3=∠5
从而得到∠4=∠5
即：AD为△ABC的角平分线

知识点：平行线的性质  全等三角形的判定  

题干中有：点E是BC中点，想到用倍长中线的方法来构造出全等三角形来转移线段和角度，从而利用题干中的平行条件求解

倍长中线

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>