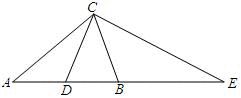
如图,CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB.求证:①CE=2CD.②CB平分∠DCE.
答案

证明:延长CD至F,使DF=CD,连结BF.
在△ADC和△BDF中,
∴△ADC≌△BDF(SAS)
∴∠A=∠ABF
又∵AC=AB
∴∠ACB=∠ABC
从而∠A+∠ACB=∠ABF+∠ABC=∠CBF
∵∠CBE是△ABC的一个外角
∴∠CBE=∠A+∠ACB
∴∠CBE=∠CBF
在△CBE和△CBF中,
∴△CBE≌△CBF(SAS)
∴CE=CF=2CD,∠BCF=∠BCE 即CB平分∠DCE
知识点:全等三角形的判定与性质
利用倍长中线法构造全等三角形,然后利用全等三角形的性质和判定定理得出结论.
不会利用倍长中线法解题








