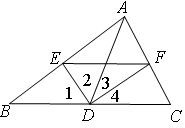
如图，AD为△ABC的中线，且∠1＝∠2，∠3＝∠4，求证：BE＋CF＞EF

答案

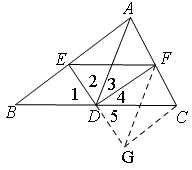
证明：延长ED到G，使得DG=DE，连接GC，GF
在△BDE和△CDG中‘

∴△BDE≌△CDG（SAS）
∴BE=CG
∵∠1=∠2=∠5，∠3=∠4
∴∠2+∠3=∠4+∠5，即∠EDF=∠GDF
在△DEF和△DGF中，

∴△DEF≌△DGF（SAS）
∴EF=FG
在△CFG中，由三角形三边关系定理可得：CF+CG>FG
由CG=BE，FG=EF得：BE+CF>EF

知识点：全等三角形的判定  

由条件，AD为△ABC的中线，想到倍长中线

倍长中线

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>