如图所示,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AE __DB(填“>”、“<”或“=”)
(2)特例启发,解答题目
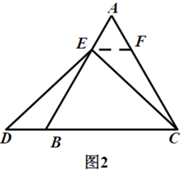
如图2,当点E为AB上的任意点时,AE__DB(填“>”、“<”或“=”).说明理由.
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).

答案
(1)∵△ABC为等边三角形,E为AB中点
∴∠ECB=30°,∠ABC=60°,AE=BE
∵DE=CE
∴∠D=∠ACB=30°
又∵∠ABC=60°=∠D+∠DEB
∴∠DEB=30°
∴∠DEB=∠D
∴BD=BE
∴BD=AE
(2)在等边三角形ABC中
∠ABC=∠ACB=60°
∴∠ABD=120°
∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠ACE
又∵ED=EC
∴∠BDE=∠ECB
∴∠BED=∠ACE
∵EF∥BC
∴∠AEF=∠AFE=60°=∠BAC
∴△AEF是正三角形,∠EFC=180°-∠ACB=120°=∠ABD
∴△EFC≌△DBE
∴DB=EF
∵EF=AE
∴AE=BD
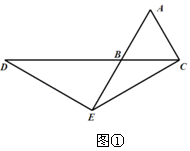
(3)第一种情况,如右图①
由前面可知,BD=AE=2
∴CD=BD+CB=2+1=3
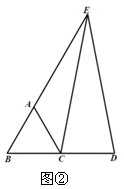
第二种情况,如右图②
由前面可知,BD=AE=2
∴CD=BD-CB=2-1=1
知识点:全等三角形的判定 轴对称-最短路线问题
(1)根据等边三角形的性质和三角形的内角和定理求出∠D=∠DEB=30°,推出DB=BE=AE即可得到答案;
(2)作EF∥BC,证出等边三角形AEF,再证△DBE≌△EFC即可得到答案;
(3)分为两种情况:一是如上图在AB边上,在CB的延长线上,求出CD=3,二是在BC上求出CD=1,即可得到答案.
思路不清晰,不会类比推理。









