在锐角△ABC中，AB=
,∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD、AB上的动点，则BM+MN的最小值是________．
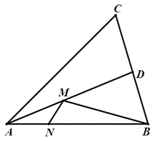
答案
4
知识点：等腰三角形的性质 轴对称-最短路线问题
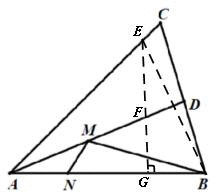
在AC线上取一点E使AE=AB.自E点向AB作垂线交AD于F、交AB于G;连接BE、BF、EM.
ABE为等腰三角形，AD为∠A的平分线，则AD必为BE的垂直平分线，故BF=EF、 BM=EM。
则BM+MN>EM+MN≥EG;只有当M点与F点重合、N点与G点重合时，BM+MN=EF+FG=EG.
因为△AEG为等腰直角三角形，AE=AB=,所以EG=
=4.得BM+MN≥EG,所以BM++MN的最小值是4.
没有思路
WORD格式（
