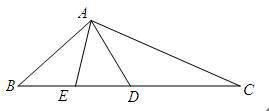
已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线。
求证：∠C=∠BAE

答案

证明：延长AE到F，使得EF=AE，

∵AE是△ABD的中线
∴BE=ED
在△ABE和△FDE中，

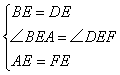
∴△ABE≌△FDE（SAS）
∴AB=FD，∠BAF=∠F，∠B=∠FDE
∵CD=AB
∴CD=FD
∵∠BDA=∠BAD
∴∠ADF=∠BDA+∠FDE，∠ADC=∠B+∠BAD
即∠ADF=∠ADC
在△FAD和△CAD中，

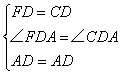
∴△FAD≌△CAD（SAS）
∴∠F=∠C
∴∠C=∠BAE

知识点：三角形全等之倍长中线  

略

略

下载次数：5

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>