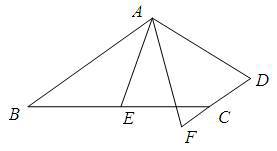
在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F.试探究线段AB与AF、CF之间的数量关系，并证明你的结论。
答案
解：AB=AF+CF，
证明如下：延长AE交DC的延长线与点G，
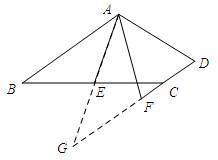
∵E为BC边的中点
∴BE=CE
∵AB∥DC
∴∠B=∠BCG，∠BAG=∠G
在△ABE和△GCE中，
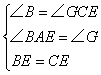
∴△ABE≌△GCE（AAS）
∴AB=GC
∵∠BAE=∠EAF
∴∠G=∠EAF
∴AF=GF
∴AB=GC=GF+FC=AF+CF
知识点：三角形全等之倍长中线
略
略
WORD格式（
