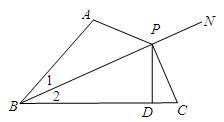
已知，如图，∠1=∠2，P为BN上一点，且PD⊥BC于点D，AB+BC=2BD.
求证：∠BAP+∠BCP=180°.

答案

证明：如图，过P做PE⊥BA交BA延长线于点E，

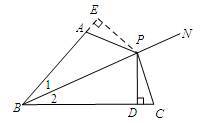
则在△BEP和△BDP中

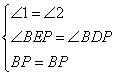
∴△BEP≌△BDP（AAS）
∴PE=PD，BE=BD
∵AB+BC=2BD
∴AB+BD+DC=BE+BD
即AB+BD+DC=AB+AE+BD
∴AE=DC
在△PAE和△PCD中

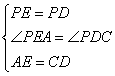
∴△PAE≌△PCD（SAS）
∴∠BCP=∠PAE
∵∠BAP+∠PAE=180°
∴∠BAP+∠BCP=180°

知识点：三角形全等之截长补短  

略

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>