已知，如图，在四边形ABCD中，BC＞AB，AD=DC，BD平分∠ABC.
求证：∠BAD+∠BCD=180°.

答案

方法一：

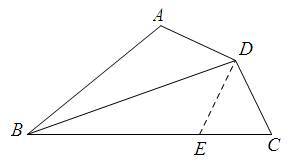
证明：在BC上截取BE，使得BE=BA，连接DE，
∵BD平分∠ABC，
∴∠ABD=∠EBD
在△ABD和△EBD中

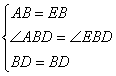
∴△ABD≌△EBD（SAS）
∴∠BAD=∠BEDAD=DE，
又∵AD=DC
∴DE=DC
∴∠DEC=∠DCE
∵∠BED+∠DEC=180°
∴∠BAD+∠BCD=180°
方法二：

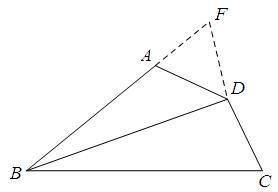
证明：延长BA至点F，使得BF=BC，连接DF，
∵BD平分∠ABC，
∴∠ABD=∠CBD
在△FBD和△CBD中

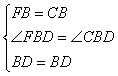
∴△FBD≌△CBD（SAS）
∴∠DFB=∠DCBFD=CD，
又∵AD=DC
∴FD=AD
∴∠DAF=∠DFB
∵∠BAD+∠DAF=180°
∴∠BAD+∠BCD=180°