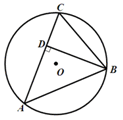
如图,已知 的半径为5,锐角△ABC内接于
的半径为5,锐角△ABC内接于 ,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )
,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )
- A.
- B.
- C.
- D.
答案
正确答案:D
知识点:垂径定理
法一:连接OA、OB,过点O做OM⊥AB,如下图,由垂径定理有AM=BM=AB=4,且
∠AOM=∠BOM=∠AOB,要求tan∠CBD,放在Rt△CDB中tan∠CBD=cot∠DCB,∠DCB=
∠AOB=∠AOM,所以tan∠CBD=cot∠AOM,在Rt△AMO中,AO=5,AM=4,勾股定理可得
OM=3,所以tan∠CBD=cot∠AOM==
法二:延长AO交于点E,连接BE,则∠AEB=∠ACB,∠ABE=90°,∵∠BAE+∠AEB=90°,
∠CBD+∠ACB=90°,∴∠CBD=∠BAE,在Rt△ABE中,AE=5×2=10,AB=8,∴BE=6,
∴tan∠CBD=tan∠BAE=
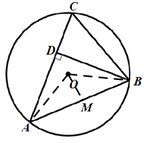
不会转移角








