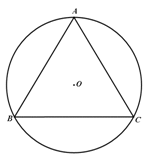
已知如图，等腰三角形ABC中，AB＝AC，半径OB＝5cm，圆心O到BC的距离为3cm，求A到BC的距离．

答案

由垂径定理的推理得，垂直弦且平分弦的弦必过圆心，是直径。
作AD⊥BC，交BC于点D，则AC必过圆心O，Rt△ODB，OB=5cm，OD=3cm，勾股定理可得BD=4，由等腰三角形三线合一的性质，AD即为A到BC的距离，AD=AO+OD＝5+3＝8cm

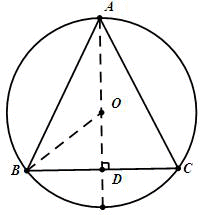
知识点：垂径定理  

由垂径定理的推理得，垂直弦且平分弦的弦必过圆心，是直径。
作AD⊥BC，交BC于点D，则AC必过圆心O，Rt△ODB，OB=5cm，OD=3cm，勾股定理可得BD=4，由等腰三角形三线合一的性质，AD即为A到BC的距离，AD=AO+OD＝5+3＝8cm

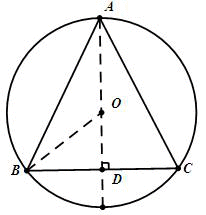
略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>