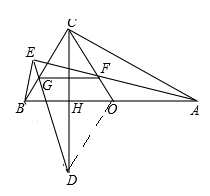
如图，O是Rt△ABC斜边AB的中点，CH⊥AB于H，延长CH至D，使得CH=DH，F为CO上任意一点，过B作BE⊥AF于E，连接DE交BC于G．求证：∠CAF=∠CDE．
答案
（1）证明：连接OD，
∵△ABC是Rt三角形，BE⊥AF
∴∠BEA=∠ACB=90°，
∴A，B，E，C，四点共圆，且AB是此圆直径，
又∵CH⊥AB，CH=DH，
∴OC=OD
∴D在此圆上，
∴A，B，C，D，E五点共圆，
∴∠CAF=∠CDE．
知识点：确定圆的条件 相似三角形的判定与性质
先连接OD，根据已知条件得出∠BEA=∠ACB=90°，得出A，B，E，C，四点共圆且AB是此圆直径，再根据CH⊥AB，CH=DH，确定出D也在此圆上，从而得出A，B，C，D，E五点共圆，即可证出∠CAF=∠CDE
略
WORD格式（
