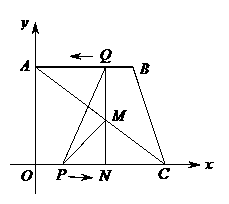
如图，直角梯形OABC中，AB∥OC，∠OAB=90°且OA=AB，点A、C的坐标分别为（0,3）、（4,0），动点P从O点出发，沿线段OC向点C作匀速运动；动点Q从点B出发，沿线段BA向点A作匀速运动．过Q点垂直于AB的射线交AC于点M，交OC于点N．P、Q两点同时出发，速度都为每秒1个单位长度．当Q点运动到A点，P、Q两点同时停止运动．设点Q运动的时间为t秒．
（1）求NC，MC的长（用含t的代数式表示）；
（2）当t为何值时，四边形PCBQ构成平行四边形？
（3）是否存在某一时刻，使射线QN恰好将△AOC的面积和周长同时平分？若存在，求出此时t的值；若不存在，请说明理由；
（4）探究：t为何值时，△PMC为等腰三角形．

答案

（1）∵AQ=ON=3-t
∴CN=4-（3-t）=1+t
在Rt△AOC中，AC²=AO²+OC²=3²+4²
∴AC=5
在Rt△MNC中，cos∠NCM=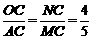，CM=．
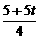（2）由于四边形PCBQ是平行四边形
∴PC=QB，即4-t=t
解得t=2．
（3）如果射线QN将△AOC的周长平分，则有：
MC+NC=，
即： $\frac{5}{4}$ （1+t）+1+t= $\frac{1}{2}$ （3+4+5）
解得：t= $\frac{5}{3}$
而MN= $\frac{3}{4}$ NC= $\frac{3}{4}$ （1+t）
∴S_△_MNC=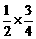（1+t）²= $\frac{3}{8}$ （1+t）²
当t= $\frac{5}{3}$ 时，S_△_MNC= $\frac{3}{8}$ （1+t）²= $\frac{8}{3}$ ≠ $\frac{1}{2}$ × $\frac{1}{2}$ ×4×3
∴不存在某一时刻t，使射线QN恰好将△AOC的面积和周长同时平分．
（4）①当MP=MC时
则有：NP=NC
即PC=2NC
∴4-t=2（1+t）
解得：t= $\frac{2}{3}$