如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，然后将△ADE绕A点顺时针旋转一定角度，得到图②，然后将BD、CE分别延长至M、N，使DM=
BD，EN=CE，得到图③.
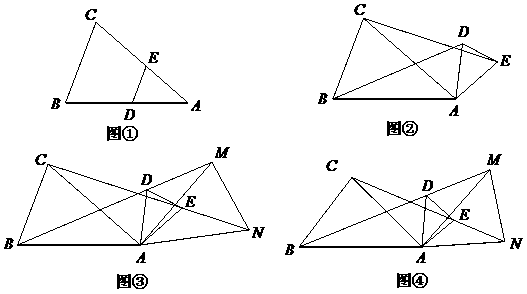
请解答下列问题：
（1）若AB=AC，请探究下列数量关系：
①在图②中，BD与CE的数量关系是 ；
②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；
（2）若AB=k•AC（k＞1），按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN与∠BAC的数量关系，直接写出你的猜想，不必证明．
答案
（1）①BD=CE
②AM=AN，∠MAN=∠BAC
.∵∠DAE=∠BAC
∴∠CAE=∠BAD
由题意可知：AB=AC，AD=AE
∴△BAD≌△CAE
∴∠ABD=∠ACE
在△ABM和△ACN中，DM=BD，EN=
CE
∴BM=CN
又∵AB=AC
∴△ABM≌△ACN
∴AM=AN，∠BAM=∠CAN
即∠BAC＋∠CAM=∠MAN+∠CAM
则∠MAN=∠BAC
（2）AM=k•AN，∠MAN=∠BAC.
知识点：全等三角形的判定
略
略
WORD格式（
