如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS,其中正确结论的序号是( )
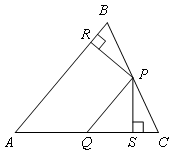
- A.①②
- B.①②③
- C.①②④
- D.①②③④
答案
正确答案:C
知识点:略
连接AP,RS,如图所示,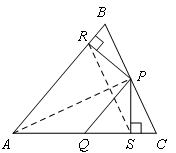
∵PR⊥AB,PS⊥AC,
∴∠ARP=∠ASP=90°,
在Rt△APR≌Rt△APS中,![]() ,
,
∴Rt△APR≌Rt△APS(HL),
∴AS=AR,∠PAR=∠PAS,故①正确,
∵AQ=PQ,
∴∠PAS=∠APQ,
∴∠PAR=∠APQ,
∴QP∥AR,故②正确,
在Rt△BRP和Rt△QSP中,只有PR=PS,
不满足三角形全等的条件,故③错误;
∵在△ARS中,AR=AS,∠PAR=∠PAS,
∴AP垂直平分RS,故④正确,
故选:C.
略





