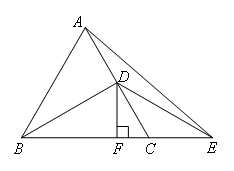
如图所示,在等边三角形ABC中,D为AC边的中点,E为边BC延长线上一点,BD=DE,DF⊥BE,垂足为点F,下列结论:①AD=CE;②CE+CD=AB;③∠BDE=120°;④CF:BF=1:3;⑤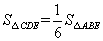 ,其中正确的有( )
,其中正确的有( )
- A.2个
- B.3个
- C.4个
- D.5个
答案
正确答案:D
知识点:略
∵△ABC是等边三角形,D为AC边的中点,
∴AD=CD,
∴BD⊥AC,BD平分∠ABC,
∵∠ABC=60°,
∴∠ABD=∠DBC=30°,
∵DB=DE,
∴∠DBC=∠DEC=30°,
∴∠BDE=120°,故③正确;
∵BD⊥AC,∠BDE=120°,
∴∠CDE=∠CED=30°,
∴CD=CE=AD,故①正确;
∵AB=AC=2CD,CD=CE,
∴CE+CD=AB,故②正确;
∵BC=AC=2CD,
∴BC=4CF,
∴BF=3CF,即CF:BF=1:3,故④正确;
∵BC=2CD=2CE,
∴![]() ,
,![]() ,
,
∵AD=CD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,故⑤正确;
,故⑤正确;
故选:D.
略





