在Rt△ABC中，∠B=90°，AB=8，AC=10，以A为圆心，AM的长为半径作弧，分别交AC，AB于点M，N；再分别以M，N为圆心，适当长度为半径画弧，两弧交于点P，连接AP，并延长AP交BC于D，过D作DE⊥AC于点E，垂足为E，则DE的长度为(    )

• A.
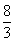
• B.
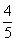
• C.2
• D.1

答案

正确答案：A

知识点：勾股定理综合应用  

由题意可得：∠EAD=∠BAD，AD平分∠BAC，
因为∠B=90°，DE⊥AC，
所以DE=DB，
因为∠B=90°，AB=8，AC=10，
所以由勾股定理得：BC==6，
因为，
所以，
解得：DE=，
故选：A．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>