如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8．P、Q是两个动点，点P从点A出发，以每秒2个单位长度的速度沿折线A-C-B的路线向终点B运动，同时点Q从点B出发，以每秒3个单位长度的速度沿折线B-C-A的路线向终点A运动，点P和点Q都运动到各自的终点时停止．设运动时间为t（秒）．直线经过点C，且∥AB，过点P，Q分别作直线的垂线，垂足为E，F，当△CPE与△CQF全等时，t的值不可能是(    )

①当P在AC上，Q在BC上时，如图所示，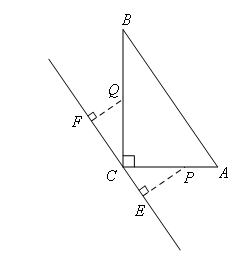

∵∠ACB=90，
∴∠PCE+∠QCF=90°，
∵PE⊥于E，QF⊥于F．
∴∠EPC+∠PCE=90°，∠PEC=∠CFQ=90°，
∴∠EPC=∠QCF，
∴当△CPE与△CQF全等时，PC=CQ，
∴6-2t=8-3t，
解得：t=2；
②当P在AC上，Q在AC上时，如图所示，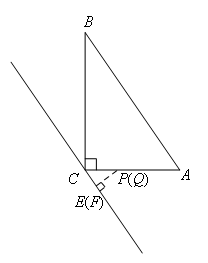

△CPE与△CQF全等时P、Q重合，CQ=PC，
由题意得，6-2t=3t-8，
解得：t=2.8；
③当P在BC上，A、Q重合时，如图所示，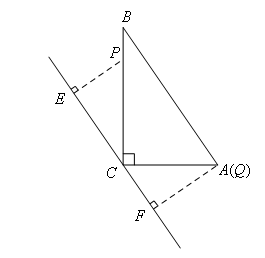

△CPE与△CQF全等，CQ=AC=6，
由题意得，2t-6=6，
解得：t=6．
综上，当△CPE与△CQF全等时，t的值为2或2.8或6，
故选：C．

略