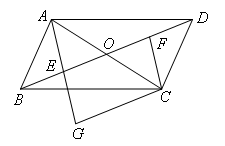
如图，在□ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至G，使EG=AE，连接CG．下列说法：①△ABE≌△CDF；②当OA=OE时，四边形AECF是矩形；③当AC=2AB时，四边形EGCF是矩形．其中正确的个数是(    )

①∵四边形ABCD是平行四边形
∴AO=CO，BO=OD，AB=CD，AB∥CD
∴∠ABE=∠CDF
∵点E，F分别为OB，OD的中点
∴
∴△ABE≌△CDF（SAS），正确
②由①得△ABE≌△CDF
∴AE=CF，∠AEB=∠CFD
∴∠GEF=∠AEB=∠CFD
∴AE∥CF
∴四边形AECF是平行四边形
∴OE=OF，OA=OC
∵OA=OE
∴OA=OE=OC=OF即EF=AC
∴□AECF为矩形，正确
③∵EG=AE由②得
GE∥CF且GE=CF
∴四边形EGCF是平行四边形
∵AC=2AB
∴AO=AB
则△ABO中可得AE⊥OB，故∠OEG=90°
∴□EGCF为矩形，正确．
综上，正确的为①②③．

略