如图，在菱形ABCD中，∠A=60°，E是AB边上一动点（不与A，B重合），且∠EDF=∠A，则下列结论不一定正确的是(    )

如图，连接BD，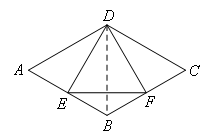

∵四边形ABCD是菱形，∠A=60°
∴AB=AD=CD=BC，∠C=∠A=60°
∴△ABD和△BCD均为等边三角形
∴AD=BD，∠DBF=60°
∵∠ADE+∠BDE=60°，∠BDF+∠BDE=∠EDF=60°
∴∠ADE=∠BDF
在△ADE和△BDF中，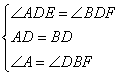

∴△ADE≌△BDF
∴DE=DF，AE=BF，故A正确
∵∠EDF=∠A=60°
∴△DEF是等边三角形，故C正确
∴∠DEF=60°
∵∠DEB=∠A+∠ADE=60°+∠ADE，
∠DEB=∠DEF+∠BEF=60°+∠BEF
∴∠ADE=∠BEF，故B正确
∵△ADE≌△BDF
∴AE=BF，则BE=CF
∴△BEF不一定是等腰三角形，故D错误

略