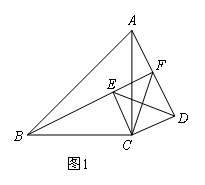
（2021武汉）问题提出
如图1，在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=AC，EC=DC，点E在△ABC内部，直线AD与BE交于点F．线段AF，BF，CF之间存在怎样的数量关系？
问题探究
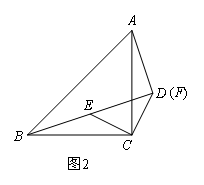
（1）先将问题特殊化如图2，当点D，F重合时，直接写出一个等式，表示AF，BF，CF之间的数量关系；
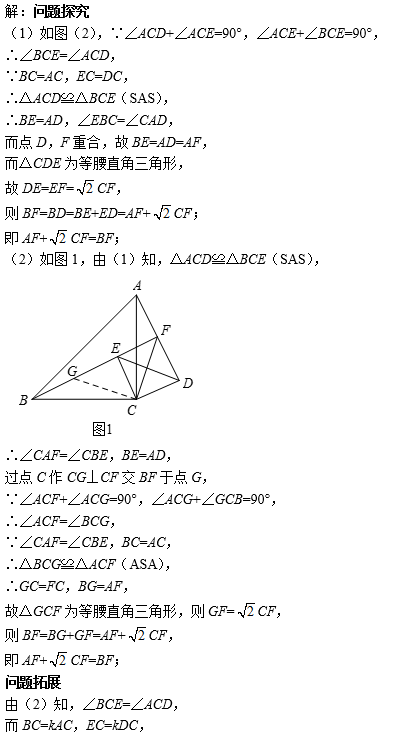
（2）再探究一般情形如图1，当点D，F不重合时，证明1中的结论仍然成立．
问题拓展
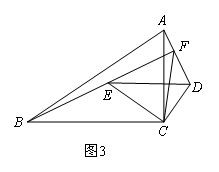
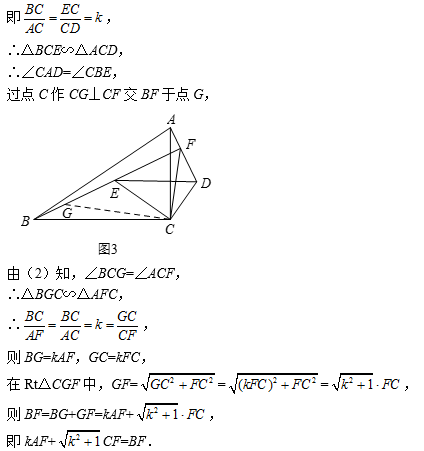
如图3，在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=kAC，EC=kDC（k是常数），点E在△ABC内部，直线AD与BE交于点F．直接写出一个等式，表示线段AF，BF，CF之间的数量关系．

答案

问题探究：
（1）AF+CF=BF；
（2）证明略；
问题拓展：
kAF+CF=BF．

知识点：相似三角形的判定与性质  类比探究  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>