如图，直线PQ∥MN，点C是PQ，MN之间（不在直线PQ，MN上）的一个动点．
（1）若∠1与∠2都是锐角，如图1，请直接写出∠C与∠1，∠2之间的数量关系；
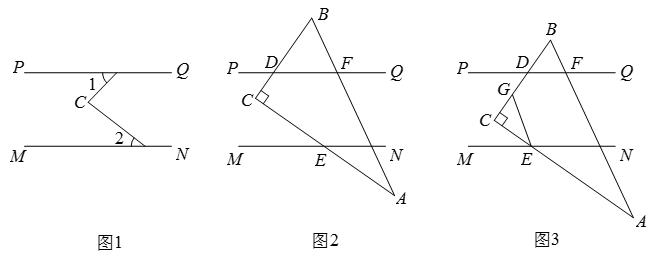
（2）若把一块三角尺（∠A=30°，∠C=90°）按如图2方式放置，点D，E，F是三角尺的边与平行线的交点，若∠AEN=∠A，求∠BDF的度数；
（3）将图2中的三角尺进行适当转动，如图3，直角顶点C始终在两条平行线之间，点G在线段CD上，连接EG，且有∠CEG=∠CEM，求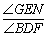的值．

解：（1）∠C＝∠1+∠2．
理由：如图，过C作CD∥PQ，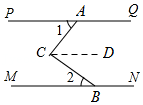

因为PQ∥MN，
所以PQ∥CD∥MN，
所以∠1＝∠ACD，∠2＝∠BCD，
所以∠ACB＝∠ACD+∠BCD＝∠1+∠2．
（2）因为∠AEN＝∠A＝30°，
所以∠MEC＝30°，
由（1）可得，∠C＝∠MEC+∠PDC＝90°，
所以∠PDC＝90°﹣∠MEC＝60°，
所以∠BDF＝∠PDC＝60°；
（3）设∠CEG＝∠CEM＝x，则∠GEN＝180°﹣2x，
由（1）可得，∠C＝∠CEM+∠CDP，
所以∠CDP＝90°﹣∠CEM＝90°﹣x，
所以∠BDF＝90°﹣x，
所以．

略