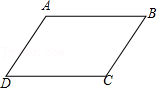
我们已经学过了对顶角、同位角等，知道了它们的特征．现在若有两个角，它们不是同一个顶点，但这两角的两边相互平行，我们就把满足这个条件的两个角称作“平行角”．如图1，已知AB∥CD，AD∥BC，因此∠B和∠D是“平行角”．
（1）图1中，证明∠B=∠D；
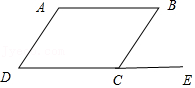
（2）如图2，延长DC到E，可知∠A和∠BCE也是“平行角”，判断它们的数量关系；
（3）如图3，DE平分∠ADC，BF平分∠ABC，请说明图中的∠1和∠2是“平行角”．
答案
（1）证明略°；
（2）∠A+∠BCE=180°；
（3）略．
（1）证明：因为AB∥CD，AD∥BC，
所以∠D+∠A＝180°，∠B+∠A＝180°．
所以∠B＝∠D．
（2）解：由（1）知∠B＝∠D，
同理可得，∠A＝∠BCD.
因为∠BCD+∠BCE＝180°，
所以∠A+∠BCE＝180°．
即∠A和∠BCE互补．
（3）证明：因为∠B和∠D是“平行角”，
所以∠ABC＝∠ADC．
因为DE平分∠ADC，BF平分∠ABC
所以∠1=
∠ADC，∠2=∠ABC．
所以∠1＝∠2．
又因为AB∥DC，
所以∠2＝∠BFC．
所以∠1＝∠BFC．
所以DE∥BF．
所以∠1和∠2是“平行角”．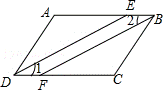
略
WORD格式（
