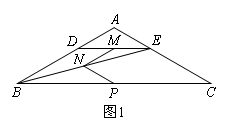
（2020东营）如图1，在等腰三角形ABC中，∠A=120°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接BE，点M，N，P分别为DE，BE，BC的中点．
（1）观察猜想
图1中，线段NM，NP的数量关系是        ，∠MNP的大小为        ；
（2）探究证明
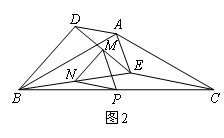
把△ADE绕点A顺时针方向旋转到如图2所示的位置，连接MP，BD，CE，判断△MNP的形状，并说明理由；
（3）拓展延伸
把△ADE绕点A在平面内自由旋转，若AD=1，AB=3，请求出△MNP面积的最大值．

答案

（1）NM=NP；60°；
（2）△MNP是等边三角形，理由略；
（3）△MNP面积的最大值为．

知识点：中点  旋转  几何最值  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>