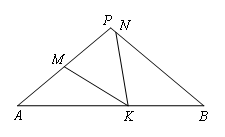
如图，在△PAB中，PA=PB，∠APB=100°，点M，N，K分别是PA，PB，AB上的点，若MK=KN，∠MKN=40°，求证：AM+BN=AB．

证明：
∵PA=PB，∠APB=100°，
∴∠A=∠B=40°，∠AMK+AKM=140°，
∵∠MKN=40°，
∴∠AKM+∠BKN=140°，
∴∠AMK=∠BKN
又∵MK=KN，
∴△AMK≌△BKN（AAS），
∴AM=BK，AK=BN，
∴AB=AK+BK=AM+BN．
即AM+BN=AB．

略