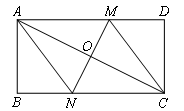
（2020大庆）如图，在矩形ABCD中，O为对角线AC的中点，过点O作直线分别与矩形的边AD，BC交于M，N两点，连接CM，AN．
（1）求证：四边形ANCM为平行四边形；
（2）若AD=4，AB=2，且MN⊥AC，求DM的长．

解：（1）证明：∵在矩形ABCD中，O为对角线AC的中点，
∴AD∥BC，AO=CO，
∴∠OAM=∠OCN，∠OMA=∠ONC，
在△AOM和△CON中，

∴△AOM≌△CON（AAS），
∴AM=CN，
∵AM∥CN，
∴四边形ANCM为平行四边形．
（2）∵在矩形ABCD中，AD=BC，
由（1）知：AM=CN，
∴DM=BN，
∵四边形ANCM为平行四边形，MN⊥AC，
∴平行四边形ANCM为菱形，
∴AM=AN=NC=AD-DM，
∴在Rt△ABN中，根据勾股定理，得
AN²=AB²+BN²，
∴(4-DM)²=2²+DM²，
解得DM=．

略